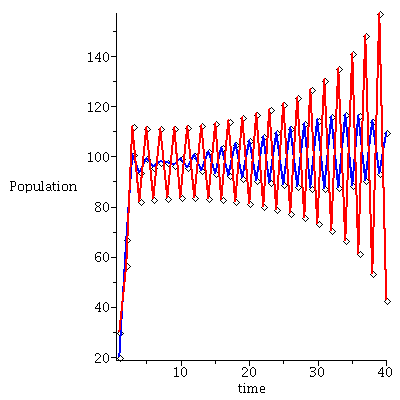
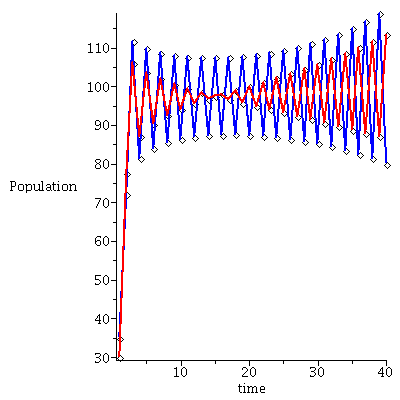
| > |
 `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0">
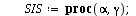 `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0">
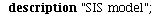 `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0">
 `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0">
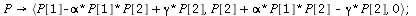 `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0">
 `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> `(`+`(P[1], `-`(`*`(alpha, `*`(P[1], `*`(P[2])))), `*`(gamma, `*`(P[2]))), `+`(P[2], `*`(alpha, `*`(..." align="center" border="0"> |
![VectorCalculus:-`+`(P[2], VectorCalculus:-`*`(VectorCalculus:-`*`(alpha, P[2]), VectorCalculus:-`+`(VectorCalculus:-`+`(N, VectorCalculus:-`-`(VectorCalculus:-`*`(gamma, `/`(1, `*`(alpha))))), VectorC...](images/SIS_74.gif)
![`+`(P[2], `*`(alpha, `*`(P[2], `*`(`+`(N, `-`(`/`(`*`(gamma), `*`(alpha))), `-`(P[2])))))) = `+`(P[2], `*`(alpha, `*`(`+`(N, `-`(`/`(`*`(gamma), `*`(alpha)))), `*`(P[2](`+`(1, `-`(`/`(`*`(P[2]), `*`(`...](images/SIS_75.gif)
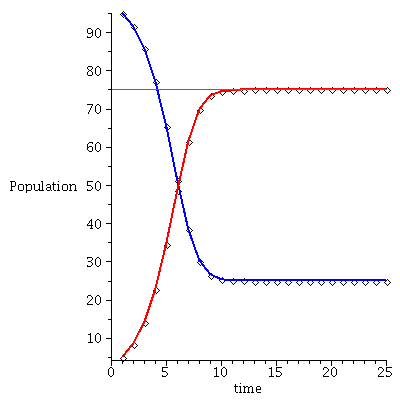
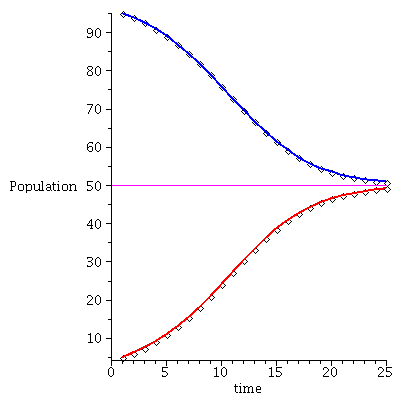
, Vector[column](%id = 135338164)](images/SIS_113.gif)
, Vector[column](%id = 141281052)](images/SIS_131.gif)