Interspecific competition 

If you click on !!! (the menu bar at the top) maple will execute all commands.  

You can also enter each command as you go along  reading this document. You may enter your own commands at any time and place in this document. 

> restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
restart; -1; with(LinearAlgebra); -1; with(plots); -1; with(VectorCalculus); -1; `:=`(LV, proc (K, r, s, u, v) option operator; description
 

The model for interspecific competition is 

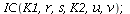> IC(K1, r, s, K2, u, v); 1
 

proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(r, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vecto...
proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(r, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vecto...		 (1)
 

and the equilibria for this model are 

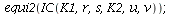> equi2(IC(K1, r, s, K2, u, v)); 1
 

 

 

 

 

 

`*`(The, `*`(equilibria, `*`(are)))
[[P[1] = 0, P[2] = 0], [P[1] = K1, P[2] = 0], [P[1] = 0, P[2] = K2], [P[1] = `+`(`-`(`/`(`*`(`+`(K1, `-`(`*`(s, `*`(K2))))), `*`(`+`(`-`(1), `*`(s, `*`(v))))))), P[2] = `/`(`*`(`+`(`-`(K2), `*`(v, `*`...
`*`(The, `*`(eigenvalues, `*`(are)))
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
Vector[column](%id = 138486548), Vector[column](%id = 138980500), Vector[column](%id = 139223892), Vector[column](%id = 139231616)
`*`(The, `*`(absolute, `*`(values, `*`(of, `*`(the, `*`(eigenvalues, `*`(are)))))))
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)
Vector[column](%id = 135574748), Vector[column](%id = 135558912), Vector[column](%id = 136279208), Vector[column](%id = 137776728)		 (2)
 

Well, this becomes a little confusing. 

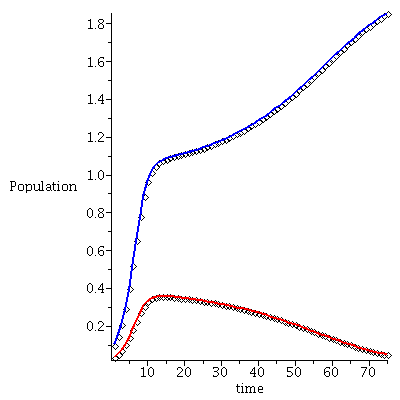
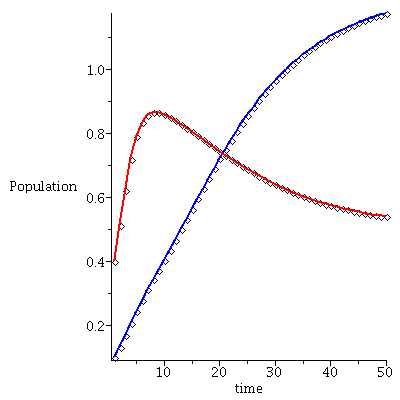
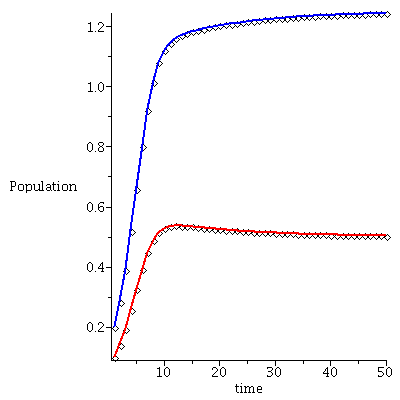
In the following we consider models with K1=2, K2=1, and r=0.5, u=0.5. The two remaining parameters, s and v, will be chosen so that in  

Case 1: One species will dominate (independent of the initial population phase) 

Case 2: Either one of the two species may dominate depending on the initial population phase 

Case 3: The two species will coexist 

Case 1. One species will dominate.  

When s<K1/K2=2 and v>K2/K1=1/2, species 1 will dominate. 

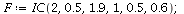> `:=`(F, IC(2, .5, 1.9, 1, .5, .6)); 1
 

proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...
proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...		 (3)
 

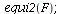> equi2(F); 1
 

 

 

 

 

 

`*`(The, `*`(equilibria, `*`(are)))
[[P[1] = 0., P[2] = 0.], [P[1] = 2., P[2] = 0.], [P[1] = 0., P[2] = 1.], [P[1] = -.7142857143, P[2] = 1.428571429]]
`*`(The, `*`(eigenvalues, `*`(are)))
Vector[column](%id = 140847276), Vector[column](%id = 140911408), Vector[column](%id = 140962956), Vector[column](%id = 136824012)
Vector[column](%id = 140847276), Vector[column](%id = 140911408), Vector[column](%id = 140962956), Vector[column](%id = 136824012)
`*`(The, `*`(absolute, `*`(values, `*`(of, `*`(the, `*`(eigenvalues, `*`(are)))))))
Vector[column](%id = 141090032), Vector[column](%id = 141090104), Vector[column](%id = 141090176), Vector[column](%id = 141090248) (4)
 

> display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.9, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.9, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
 

Plot_2d
 

> display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.9, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.9, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
 

Plot_2d
 

> display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-1, j)), j = 1 .. 10)}, {seq(`<,>`(VectorCalculus:-`+`(.4, VectorCalculus:-`*`(.1, j)), 1.1), j = 1 .. 20)})), dir...
display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-1, j)), j = 1 .. 10)}, {seq(`<,>`(VectorCalculus:-`+`(.4, VectorCalculus:-`*`(.1, j)), 1.1), j = 1 .. 20)})), dir...
display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-1, j)), j = 1 .. 10)}, {seq(`<,>`(VectorCalculus:-`+`(.4, VectorCalculus:-`*`(.1, j)), 1.1), j = 1 .. 20)})), dir...
 

Plot_2d
 

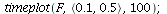> timeplot(F, `<,>`(.1, .5), 100); 1
 

Plot_2d
 

When s>K1/K2=2 and v<K2/K1=1/2, species 2 will dominate. 

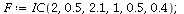> `:=`(F, IC(2, .5, 2.1, 1, .5, .4)); 1
 

proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...
proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...		 (5)
 

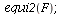> equi2(F); 1
 

 

 

 

 

 

`*`(The, `*`(equilibria, `*`(are)))
[[P[1] = 0., P[2] = 0.], [P[1] = 2., P[2] = 0.], [P[1] = 0., P[2] = 1.], [P[1] = -.6250000000, P[2] = 1.250000000]]
`*`(The, `*`(eigenvalues, `*`(are)))
Vector[column](%id = 143115228), Vector[column](%id = 144943524), Vector[column](%id = 141299084), Vector[column](%id = 143834716)
Vector[column](%id = 143115228), Vector[column](%id = 144943524), Vector[column](%id = 141299084), Vector[column](%id = 143834716)
`*`(The, `*`(absolute, `*`(values, `*`(of, `*`(the, `*`(eigenvalues, `*`(are)))))))
Vector[column](%id = 145031328), Vector[column](%id = 143711356), Vector[column](%id = 143947100), Vector[column](%id = 144060116) (6)
 

> display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.1, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.1, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
 

Plot_2d
 

> display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.1, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.1, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
 

Plot_2d
 

> display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(VectorCalculus:-`*`(.1, i), .1), i = 1 .. 15)}, {seq(`<,>`(2.1, VectorCalculus:-`*`(.1, j)), j = 1 .. 10)})), dirfield(F, 2.1, 1.1), implicitp...
display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(VectorCalculus:-`*`(.1, i), .1), i = 1 .. 15)}, {seq(`<,>`(2.1, VectorCalculus:-`*`(.1, j)), j = 1 .. 10)})), dirfield(F, 2.1, 1.1), implicitp...
display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(VectorCalculus:-`*`(.1, i), .1), i = 1 .. 15)}, {seq(`<,>`(2.1, VectorCalculus:-`*`(.1, j)), j = 1 .. 10)})), dirfield(F, 2.1, 1.1), implicitp...
 

Plot_2d
 

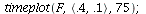> timeplot(F, `<,>`(.4, .1), 75); 1
 

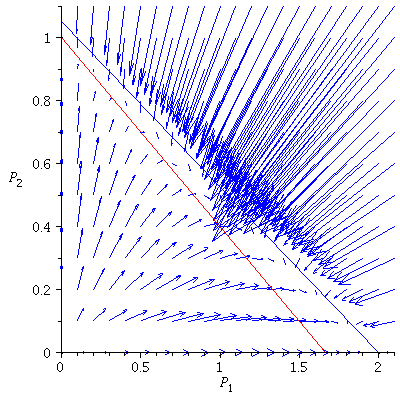
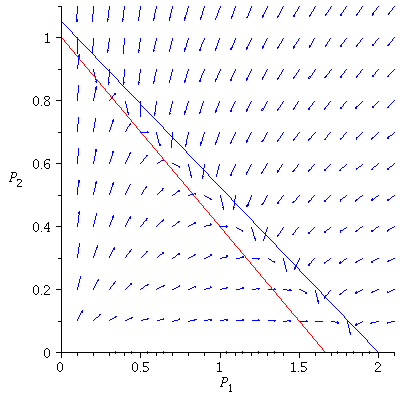
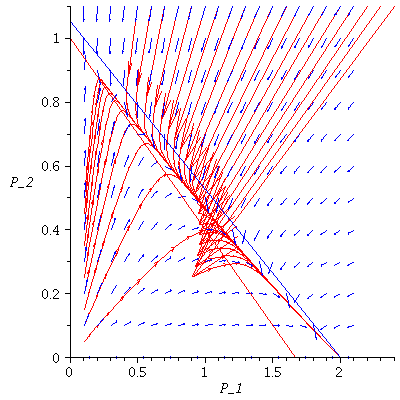
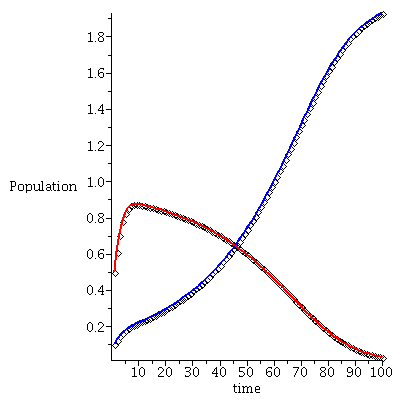
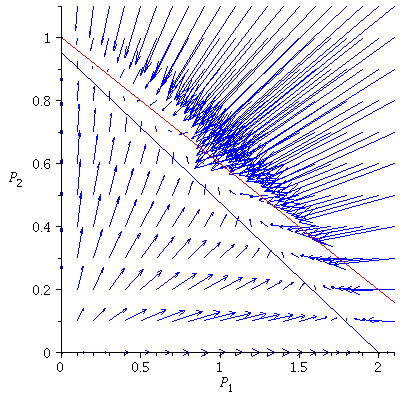
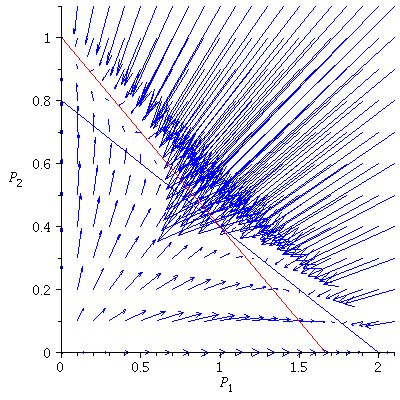
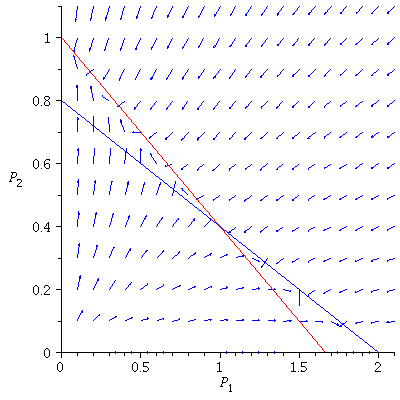
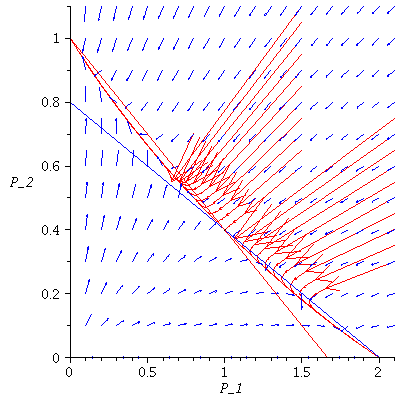
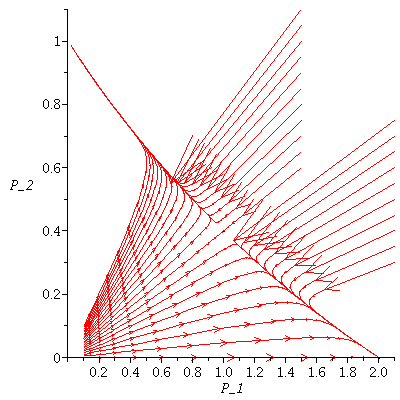
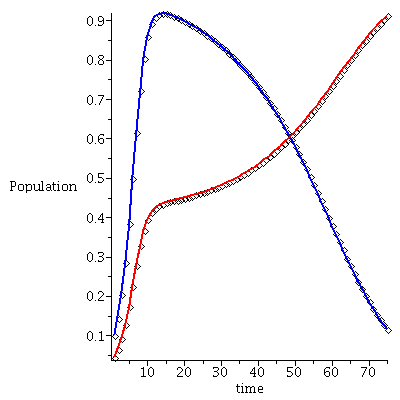
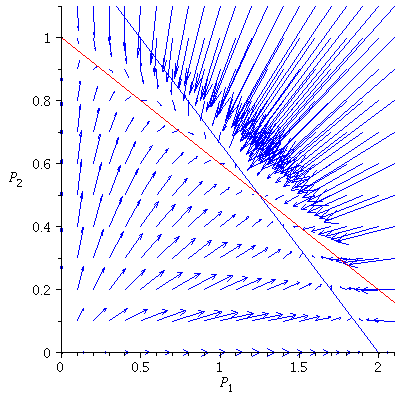
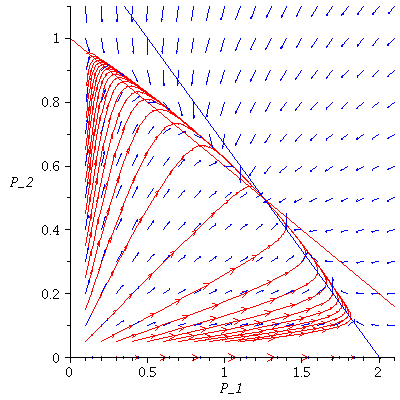
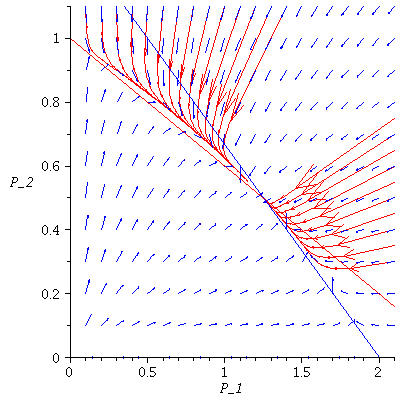
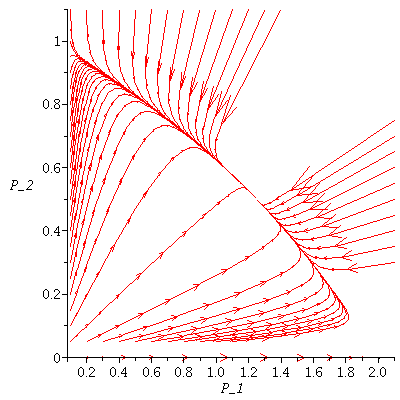
Plot_2d
 

Case 2. Both species may dominate. 

When s>K1/K2=2 and v>K2/K1=1/2, both species may dominate, the outcome of the competition depends on the initial population phase.  

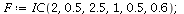> `:=`(F, IC(2, .5, 2.5, 1, .5, .6)); 1
 

proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...
proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...		 (7)
 

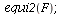> equi2(F); 1
 

 

 

 

 

 

`*`(The, `*`(equilibria, `*`(are)))
[[P[1] = 0., P[2] = 0.], [P[1] = 2., P[2] = 0.], [P[1] = 0., P[2] = 1.], [P[1] = 1., P[2] = .4000000000]]
`*`(The, `*`(eigenvalues, `*`(are)))
Vector[column](%id = 138188772), Vector[column](%id = 138534836), Vector[column](%id = 138659052), Vector[column](%id = 138837616)
Vector[column](%id = 138188772), Vector[column](%id = 138534836), Vector[column](%id = 138659052), Vector[column](%id = 138837616)
`*`(The, `*`(absolute, `*`(values, `*`(of, `*`(the, `*`(eigenvalues, `*`(are)))))))
Vector[column](%id = 138866008), Vector[column](%id = 138864512), Vector[column](%id = 138858376), Vector[column](%id = 138852108) (8)
 

> display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
 

Plot_2d
 

> display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.6, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
 

Plot_2d
 

> display(seq(phasedia(F, P0, 50), P0 = {seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-2, j)), j = 0 .. 20)}), dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.5, P[2])) = 2...
display(seq(phasedia(F, P0, 50), P0 = {seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-2, j)), j = 0 .. 20)}), dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(2.5, P[2])) = 2...
 

Plot_2d
 

> display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(1.5, VectorCalculus:-`+`(.6, Vect...
display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(1.5, VectorCalculus:-`+`(.6, Vect...
display(seq(phasedia(F, P0, 100), P0 = `union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(1.5, VectorCalculus:-`+`(.6, Vect...
 

Plot_2d
 

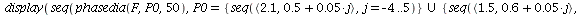
> display(seq(phasedia(F, P0, 50), P0 = `union`(`union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(1.5, VectorCalculus:-`+`(....
display(seq(phasedia(F, P0, 50), P0 = `union`(`union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(1.5, VectorCalculus:-`+`(....
 

Plot_2d
 

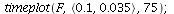> timeplot(F, `<,>`(.1, 0.35e-1), 75); 1
 

Plot_2d
 

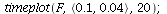> timeplot(F, `<,>`(.1, 0.4e-1), 20); 1
 

Plot_2d
 

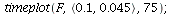> timeplot(F, `<,>`(.1, 0.45e-1), 75); 1
 

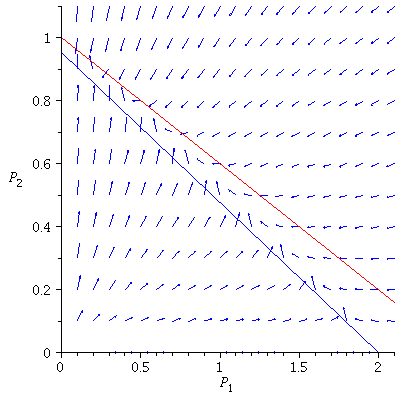
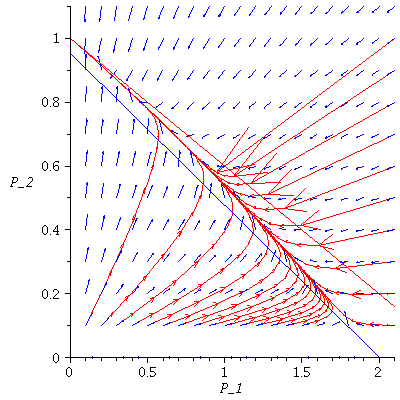
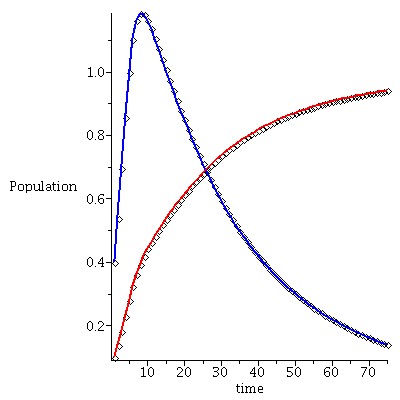
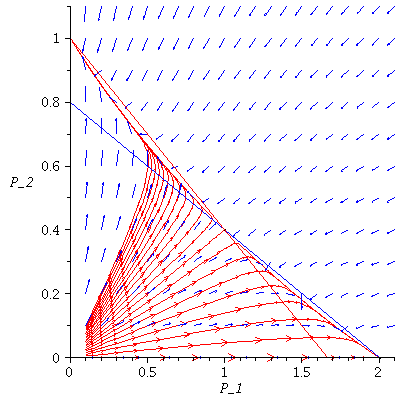
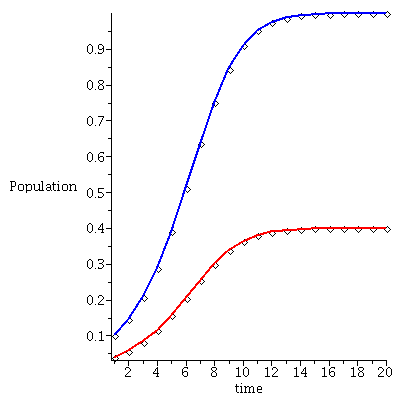
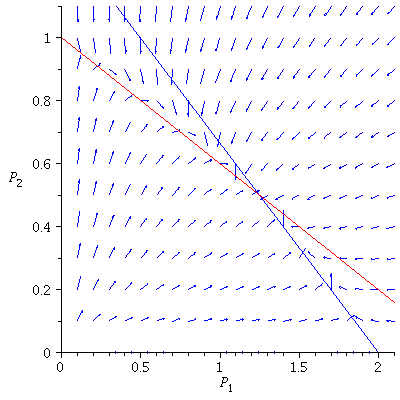
Plot_2d
 

Case 3. The two species will coexist. 

When s<K1/K2=2 and v<K2/K1=1/2, the two species will coexist. 

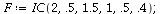> `:=`(F, IC(2, .5, 1.5, 1, .5, .4)); 1
 

proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...
proc (P) options operator, arrow; VectorCalculus:-`<,>`(VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(VectorCalculus:-`*`(.5, P[1]), VectorCalculus:-`+`(1, VectorCalculus:-`-`(VectorCalculus:-`*`(Vect...		 (9)
 

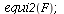> equi2(F); 1
 

 

 

 

 

 

`*`(The, `*`(equilibria, `*`(are)))
[[P[1] = 0., P[2] = 0.], [P[1] = 2., P[2] = 0.], [P[1] = 0., P[2] = 1.], [P[1] = 1.250000000, P[2] = .5000000000]]
`*`(The, `*`(eigenvalues, `*`(are)))
Vector[column](%id = 143919808), Vector[column](%id = 145964304), Vector[column](%id = 139251140), Vector[column](%id = 141077552)
Vector[column](%id = 143919808), Vector[column](%id = 145964304), Vector[column](%id = 139251140), Vector[column](%id = 141077552)
`*`(The, `*`(absolute, `*`(values, `*`(of, `*`(the, `*`(eigenvalues, `*`(are)))))))
Vector[column](%id = 141005672), Vector[column](%id = 141005736), Vector[column](%id = 141720132), Vector[column](%id = 143657576) (10)
 

> display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
display(growth(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. 1....
 

Plot_2d
 

> display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
display(dirfield(F, 2.1, 1.1), implicitplot([VectorCalculus:-`+`(P[1], VectorCalculus:-`*`(1.5, P[2])) = 2, VectorCalculus:-`+`(VectorCalculus:-`*`(.4, P[1]), P[2]) = 1], P[1] = 0 .. 2.1, P[2] = 0 .. ...
 

Plot_2d
 

> display(seq(phasedia(F, P0, 50), P0 = `union`({seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-1, j)), j = 0 .. 19)}, {seq(`<,>`(VectorCalculus:-`+`(.2, VectorCalculus:-`*`(.1, i)), 0.5e-1), i = 0 .. 9)})), di...
display(seq(phasedia(F, P0, 50), P0 = `union`({seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-1, j)), j = 0 .. 19)}, {seq(`<,>`(VectorCalculus:-`+`(.2, VectorCalculus:-`*`(.1, i)), 0.5e-1), i = 0 .. 9)})), di...
display(seq(phasedia(F, P0, 50), P0 = `union`({seq(`<,>`(.1, VectorCalculus:-`*`(0.5e-1, j)), j = 0 .. 19)}, {seq(`<,>`(VectorCalculus:-`+`(.2, VectorCalculus:-`*`(.1, i)), 0.5e-1), i = 0 .. 9)})), di...
 

Plot_2d
 

> display(seq(phasedia(F, P0, 20), P0 = `union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(VectorCalculus:-`*`(.1, i), 1.1), ...
display(seq(phasedia(F, P0, 20), P0 = `union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(VectorCalculus:-`*`(.1, i), 1.1), ...
display(seq(phasedia(F, P0, 20), P0 = `union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(VectorCalculus:-`*`(.1, i), 1.1), ...
 

Plot_2d
 

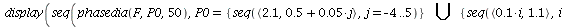
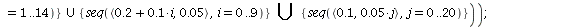> display(seq(phasedia(F, P0, 50), P0 = `union`(`union`(`union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(VectorCalculus:-`*...
display(seq(phasedia(F, P0, 50), P0 = `union`(`union`(`union`({seq(`<,>`(2.1, VectorCalculus:-`+`(.5, VectorCalculus:-`*`(0.5e-1, j))), j = VectorCalculus:-`-`(4) .. 5)}, {seq(`<,>`(VectorCalculus:-`*...
 

Plot_2d
 

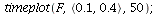> timeplot(F, `<,>`(.1, .4), 50); 1
 

Plot_2d
 

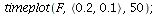> timeplot(F, `<,>`(.2, .1), 50); 1
 

Plot_2d
 

>