To study these problems I have specialized in the following areas of
mathematics:
analysis, functional analysis, ordinary and partial differential equations,
spectral theory.
- Sizes of Atoms:
Why are all atoms of
comparable sizes?
For a discussion of the empirical radius of atoms see Mark
Winther's Webelements
If you do not think that atoms are of realtively comparable
sizes, consider the fact that Sodium (Na) with eleven electrons has
essentally the same empirical radius as uranium (U) with 92
electrons (the empirical radius of Na is 180pm and the empirical
radius of U is 175pm)
The papers
[2,3,4,5,7,12,13,28,33] from my publication
list are on this subject. One particular, point proved in [33] is
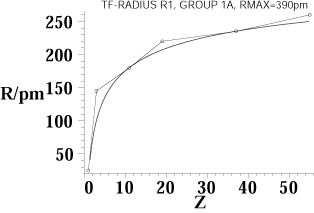
that the radius of atoms may be well estimated by what is called
Thomas-Fermi theory. The picture below illustrates this. The
circles are empirical values of the radius whereas the solid curve
is calculated using Thomas-Fermi theory
- Stability of Matter:
An article from Science News Oct. 14 1995 about research I have been
involved with concerning Stability of Matter.
More details
about this subject can be found in my review Stability of Matter,
Encyclopedia of Mathematical Physics, eds. J.-P. Francoise, G.L. Naber
and Tsou S.T. Oxford: Elsevier, 2006 (ISBN 978-0-1251-2666-3), volume
5 pages 8--14.
The papers [23,25,31,32,34,45,47,49,51,57,63,64] are on this subject.
- Magnetic fields: I have studied the structure of atoms, molecules
and matter in strong magnetic fields. The papers
[14,15,16,17,22,24,25,29,30,31,32,35,36,37,43,44] are on this subject.
- Semiclassical eigenvalue estimates: This mathematical subject is a
useful tool in many applications in atomic, molecular, and condensed
matter physics. The relevant papers are
[9,17,20,27,29,30,41,42,43,44,65]
- Mean field approximations,
Correlation estimates. Relevant papers:
[18,19,21,23,26,33,49,55,58,60,61,62]
- Bose gases: Condensation and
Bogolubov theory. This is explained in detail in the monograph
Elliott H. Lieb, Robert Seiringer, J.P. Solovej, and J. Yngvason,
The Mathematics of the Bose Gas and its Condensation. Series:
Oberwolfach Seminars, Vol. 34, 2005, VIII, 208 p., ISBN:
3-7643-7336-9. A Birkhäuser textbook.
Relevant papers are: [38,40,45,46,48,49,52,59]
