#include <models.h>
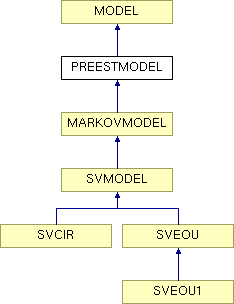
Inheritance diagram for PREESTMODEL:

Public Member Functions | |
| void | setdata (matrix Y) |
| sets the data and calculates f_j(data). | |
| matrix | estfunc (matrix par) |
| the estimating function MS(2.1) | |
| double | twonorm_estfunc (matrix par) |
| Returns two-norm of estimating function with parameters given by par. | |
| matrix | sumH (matrix par) |
| MS(3.11) disregarding A(theta). | |
| double | twonorm_sumH (matrix par) |
| Returns two-norm of _approximated_ estimating function with parameters given by par. | |
| void | set_Mbar_terms (double lambda) |
| calculates and sets Mbar_terms. | |
| void | set_iter_Mbar (bool val) |
| Determines wether Mbar (time-consuming calculation) should be calculated. | |
| void | set_sumH_est (double x) |
| Sets pre-estimate of sumH to x. | |
| void | calculate_X () |
Calculates matrix 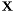 with with 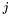 th row containing observations th row containing observations 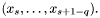 . . | |
| matrix | get_X () |
| unsigned | get_N () |
| Returns the number of inner-functions in pbef. | |
| virtual double | Zval (unsigned j, long i, long k, matrix const &Y) |
| Z_{jk}^{(i)}, j=0,...,N-1, k=1,...,q, i. | |
| double | prediction (unsigned j, long i, matrix const &Y) |
Returns 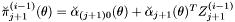 . Here . Here 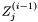 is our actual data. is our actual data. | |
Public Attributes | |
| bool | printdebug |
| boolean to determine wether to print debug-info or not | |
Protected Member Functions | |
| virtual void | calculate_Z () |
| void | calculate_a () |
Calculates the terms 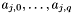 used in calculation of projections used in calculation of projections 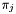 . . | |
| void | calculate_b () |
Calculates 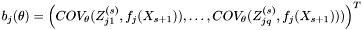 . . | |
| void | calculate_C () |
| Calculates covariance matrix of Z. | |
| void | calculate_EHH () |
The first term in the expression of 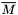 . . | |
| void | calculate_Mbar () |
Calculation of 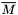 . . | |
| matrix | calculate_Dalpha () |
Partial derivatives of 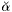 . . | |
| matrix | calculate_Cbar () |
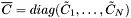 where where | |
| void | calculate_Astar () |
Calculates 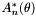 derived from Mbar,Dalpha and Cbar. derived from Mbar,Dalpha and Cbar. | |
Protected Attributes | |
| safevector< matrix > | fdata |
| matrix holding f_j(data), j=1,...,N. | |
| unsigned | N |
The number of inner-functions, 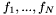 , in the estimating function. , in the estimating function. | |
| functionvector | ifuncs |
| inner-functions in estimating-function G. | |
| long | q |
| The lag-length in the prediction. | |
| long | s |
Summation start-index, 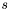 , of estimating function. , of estimating function. | |
| long | MbarNOS |
| The number of simulations used in calculating Mbar. | |
| long | l |
| summation-start in the expresion of Mbar. | |
| unsigned | numsimul |
Number of simulated variables used in determination of 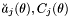 , etc. , etc. | |
| matrix | X |
For fixed 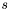 the the 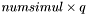 matrix with matrix with 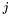 th row given by observations th row given by observations 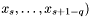 . . | |
| matrix | Xnext |
| matrix | X1 |
| bool | iter_Mbar |
| Boolean that determines wether to calculate the time-consuming Mbar in current iteration. | |
| matrix | simY |
| simulated Y for calculations. | |
| matrix | Astar |
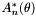 | |
| safevector< matrix > | Z |
On index j: holds simulations of 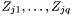 , i.e. , i.e. 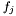 mapped onto matrix X. mapped onto matrix X. | |
| safevector< matrix > | EtildeZ |
| safevector< matrix > | fXnext |
On index j: Holds simulations of 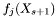 . . | |
| safevector< matrix > | fX1 |
On index j: Holds simulations of 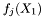 . . | |
| safevector< matrix > | a |
Terms used in projection. 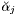 . MS(2.4). . MS(2.4). | |
| safevector< double > | a0 |
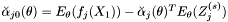 . MS(2.5) . MS(2.5) | |
| safevector< matrix > | b |
| defined (as b_j) in MS on the top of page 9. | |
| safevector< matrix > | C |
| Covariance matrix of Z_j (as C_j). See MS on the top of page 9. | |
| matrix | EHH |
| EHH in Mbar (MS(3.14)). | |
| matrix | varH |
| columnvector containing the simulated value of var(H_i) in the i'th row. | |
| double | sumH_est |
| estimate of theta, based on sumH. | |
| int | Mbar_terms |
| The number of terms in the expression of Mbar. | |
| matrix | Mbar |
| MS(3.14). | |
inherits from MODEL
Definition at line 111 of file models.h.
|
|
The first term in the expression of Iteration no. i OBS: {} has already been calculated, so we can use prediction directly without calling calculate_a(); Definition at line 239 of file models.cpp. References EHH, ifuncs, l, MbarNOS, N, prediction(), q, s, MODEL::simulate(), simY, varH, and Zval(). Referenced by calculate_Mbar().
00239 {
00240
00241 long m=l;
00242 if(q>l) m=q;
00243
00244 matrix H(N*(q+1)); // Simulation of H
00245 matrix M(N*(q+1), N*(q+1));
00246
00247 simY=simulate(MbarNOS+1);
00248
00249 for(long i=m; i<MbarNOS; i++) {
00250 //! Iteration no. i
00251
00252 for (unsigned j=0; j<N; j++) {
00253 double (*fj)(double) = ifuncs[j];
00254 for (long k=0; k<=q; k++) {
00255 //! OBS: \breve{\alpha} has already been calculated, so we can use prediction directly without calling calculate_a();
00256 double res = fj(simY.get(i))-prediction(j,i-1,simY);
00257 if (k>0) // Pr. defintion: Z_{j0}^{(i-1)} = 1
00258 res *= Zval(j,i-1,k,simY);
00259 // index (j,k) is placed in H at location (j-1)*(q+1)+k (We index from 0).
00260 unsigned Hindex = j*(q+1)+k;
00261 H.set(res,Hindex);
00262 }
00263 } // Now we have calculated H^(i)(theta)
00264
00265
00266 // Next we calculate the mean*normalization.
00267 for (unsigned r=0; r<N*(q+1); r++) {
00268 for (unsigned s=0; s<N*(q+1); s++) {
00269 M.add(H.get(r)*H.get(s),r,s); // Here we add (H*H^t)_(rs) = (H)_r*(H)_s to the matrix M.
00270 }
00271 }
00272 }
00273
00274 double w = (double)1/(double)(MbarNOS - m +1);
00275 EHH = M*w;
00276
00277 qmove(1,25);
00278 varH.newsize(N*(q+1));
00279
00280 for (unsigned k=0; k<N*(q+1); k++)
00281 varH.set(EHH.get(k,k),k); // the diagonal of E((H^r)(H^r)^T) is the
00282 // variances of the coordinates of H^r.
00283 // This is the reason why we break the
00284 // calculation of Mbar up into two pieces.
00285 }
|
 1.3.6
1.3.6